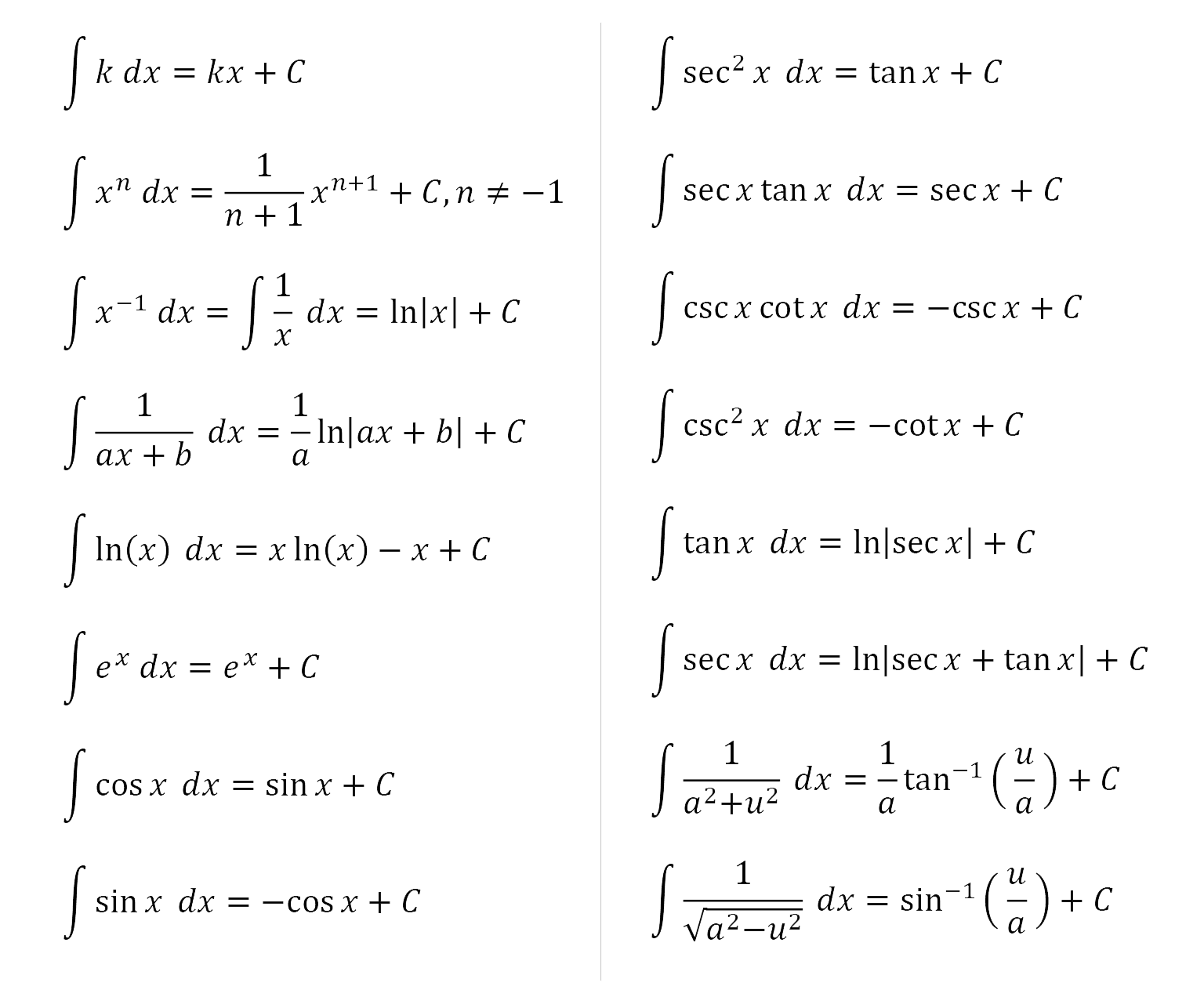Integration Rules Sheet

Integration Rules Sheet - Integration can be used to find areas, volumes, central points and many useful things. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = The first rule to know is that. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g.

∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: The first rule to know is that. Integration can be used to find areas, volumes, central points and many useful things. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points:

If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. The first rule to know is that. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. Integration can be used to find areas, volumes, central points and many useful things. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function:

Integration Rules and Formulas A Plus Topper

∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = Integration can be used to find areas, volumes, central points and many useful.

Integration Rules Cheat Sheet

∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: If < < , and (.

Integration Rules What are Integration Rules? Examples

If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: Integration can be used to find areas, volumes, central points and many useful things. ∫ f ( g ( x )) g ′ ( x.

Math for all integration farmula image

Integration can be used to find areas, volumes, central points and many useful things. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = (𝑥 ).

Integration Formulas Trig Definite Integrals Class My XXX Hot Girl

If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. The first rule to know is that. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥).

Integral cheat sheet Docsity

The first rule to know is that. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: Integration can be used to find areas, volumes, central points and many useful things. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( g ( x )) g ′ ( x ) dx = ∫.

Integration Rules and Formulas Math formula chart, Math formulas

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: Integration can.

Integration Rules Integration table Math Original

(𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = Integration can.

Integration Rules, Properties, Formulas and Methods of Integration

The first rule to know is that. Integration can be used to find areas, volumes, central points and many useful things. ∫ f ( g ( x )) g ′ ( x ) dx = ∫ f ( u ) du. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x.

Basic Integration Rules A Freshman's Guide to Integration

If (𝑥=− (−𝑥), then ∫ (𝑥) 𝑥 − =0 undefined points: The first rule to know is that. ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: ∫ f ( g ( x )) g.

Integration Can Be Used To Find Areas, Volumes, Central Points And Many Useful Things.

The first rule to know is that. (𝑥 ) 𝑥 =𝐹( )−𝐹( )=lim𝑥→ −𝐹𝑥− lim𝑥→ +𝐹(𝑥) )odd function: If < < , and ( )is undefined, then ∫ (𝑥) 𝑥 = ∫ f ( x ) g ′ ( x ) dx = f ( x ) g ( x ) − ∫ g.